Towards zero-downtime upgrades of stateful systems

Motivation

Most deployed programs need to be upgraded at some point. The reasons vary from adding new features to patching a bug and potentially fixing a broken state. Even though upgrades are an essential part of software development and maintenance, programming languages tend to not help the programmer deal with them in any way.

The situation reminds me of a remark made by Barbara Liskov about deployment of software (which is related to upgrades) in her Turing award lecture (2009):

“There’s a funny disconnect in how we write distributed programs. You write your individual modules, but then when you want to connect them together you’re out of the programming language and into this other world. Maybe we need languages that are a little bit more complete now, so that we can write the whole thing in the language.”

There’s one exception, that I know of, where upgrades are talked about from within the language: Erlang/OTP. In OTP there’s a library construct called release, which can be used to perform up- and downgrades. Furthermore, these up- and downgrades can hot swap the running code resulting in zero-downtime and no interruption of the service of connected clients.

If you haven’t seen Erlang’s hot swapping feature before, then you might want to have a look at the classic Erlang the movie, which contains a telecommunications example of this. If you prefer reading over watching, then I’ve written an earlier post which starts off by explaining a REPL session which performs an upgrade (my example isn’t nearly as cool as in the movie though).

What is it that Erlang’s releases and hot swapping facilities do? Can we steal those ideas and build upon them? These are the main questions that motivated me in writing this post.

Let’s take a step back, ignoring Erlang for a moment, and ask ourselves: what would good support for upgrades look like?

• Zero-downtime: seamless, don’t interrupt existing client connections or sessions;
• If there’s any state then migrate it in a type-safe way;
• Backwards and forwards compatibility: old clients should be able to talk to newer servers, and newer clients should be able to talk to old servers;
• Atomicity: upgrades either succeed, or fail and rollback any changes;
• Downgrades: even if an upgrade succeeds we might want to rollback to an earlier version.

In the rest of this post I’d like to explore how we can achieve some of this.

Terminology

Having defined some desirable characteristics of upgrades, let’s move on to defining what we mean by upgrades.

There are two notions I’d like clarify: what kind of software systems the upgrades are targeting, and then how we represent programs and their upgrades.

Software systems

There’s different kinds of software systems one might want to upgrade.

1. Client-only, e.g. a compiler, editor, or some command line utility which runs locally on your computer and doesn’t interact with any server. Downtime is typically not a problem, and the state of the program is typically saved to disk. The operating system’s package manager typically takes care of the upgrades, with minimal user involvement. However there are situations where one might like to perform an upgrade without first terminating the old version of a client-only application, e.g. the fix-and-continue debugging workflow from Lisp and Smalltalk, live coding music, or when working with large data sets, e.g. in bioinformatics;

2. Client-server applications where the target of the upgrade is a stateless component of the server, e.g. a front-end or a REST API. The stateless components typically retrieve the state they need to service a request from a stateful component, e.g. a database, but they don’t maintain any state of their own, which makes stateless components easier to upgrade. A common strategy is to stick a load balancer in-front of the stateless component(s), spin up the new version of the component while keeping the old version around, and then (slowly) migrate traffic over to the new version. Notice that this wouldn’t necessarily work if there was state in the components, as then the state of the old and new versions of the components might diverge and potentially have unexpected results;

3. Client-server applications where the target of the upgrade is a stateful component of the server, e.g. a database or a service with a stateful protocol like FTP. Databases were designed for supporting upgrades, with features like schema migrations and replication. The high-level idea would be to spin up the new version, take a snapshot of the old database, start logically replicating all new requests from the old to the new database while also restoring the snapshot to the new database, once the new database has caught up, we can switch over and tear down the old database. Depending on the volume of the database and the rate of new traffic this can still be a difficult operation.

   A service like FTP, where once the user is connected they can “move around” by e.g. changing the working directory and list the contents of the current working directory, are typically not possible to upgrade without downtime. The problem is that the response of one command depends on the history of previous commands in that user sessions, and this state is transient. If you think FTP is a silly protocol (it’s), then consider the similarly stateful POSIX filesystem API, with its file handles that can be opened, read, written, and closed;

4. Distributed stateful systems, e.g. a distributed key-value database. This is similar to the above, but the replication of data is performed all the time rather than only at the moment an upgrade is performed. The disadvantage is that we need more hardware and bandwidth, but on the other hand it makes upgrades much easier. Distributed systems can typically tolerate and repair some amount of faulty replicas, which allows for rolling upgrades where we replace one of the server components at the time;

5. There’s also local-first systems, which are different to all the above. I’ve not had a chance to think about upgrades in that context, so I won’t talk about them any further.

In this post I’d like to focus on upgrading stateful systems, like non-distributed databases and stateful services like FTP or filesystems.

Stateful systems arguably have the worst upgrade path of the ones listed above, making them more interesting to work on. That said I hope that the techniques can be used to simplify upgrades in the other kinds of systems too, and potentially enabling other possibilities like better debugging experience and live coding.

Programs and their upgrades

Having defined what kind of systems we’d like to upgrade, let’s turn our attention to how we can represent programs and their upgrades.

We could choose to use the syntax of a specific programming language to represent programs, but programming languages tend to be too big and complicated. Or, we could be general and represent programs as λ-calculus terms or equivalently Turing machines, but that would be too clumsy and too low-level.

A happy middle ground, which is easy to implement in any programming language while at the same time expressive enough to express any algorithm at a desired level of abstraction, is the humble state machine¹. There are different ways to define state machines, we’ll go for a definition which is a simple function from some input and a state to a pair of some output and a new state:

  input -> state -> (state, output)

where inputs, states and outputs are algebraic datatypes (records/structs and tagged unions).

To make things concrete, let’s consider an example where we represent a counter as a state machine. One way to define such a state machine is to use the enum {ReadCount, IncrCount} as input, set the state to be an integer and the output to be a tagged union where in the read case we return an integer and in the increment case we return an acknowledgment (unit or void type). Given these types, the state machine function of the counter can be defined as follows (in Python):

def counter(input: Input, state: int) -> (int, int | None):
  match input:
    case Input.ReadCount: return (state, state)
    case Input.IncrCount: return (state + 1, None)

Assuming our programs are such state machines, what would it mean to upgrade them? I think this is where having a simple representation of programs where all of the state is explicit starts to shine. By merely looking at the function type of a state machine, we can see that it would make sense to be able to:

1. Extend the input type with more cases, e.g. a ResetCount which sets the new state to 0;
2. Refine an existing output with more data, e.g. we could return the old count when we increment;
3. Extending the state, e.g. we could add a boolean to the state which determines if we should increment by +1 or -1 (i.e. decrementing);
4. Refine an existing input, e.g. make IncrCount have an integer value associated with it which determines by how much we want to increment.

I don’t know if the above list complete, but it’s a start.

If we go back to the list of criteria for good upgrade support, we can see how some of the items there are more tangible now.

For example, typed state migrations means that if we change the state type from state to state' then when we migrate to old to the new state using a function of type state -> state'.

Similarly, what it means to support backwards compatibility is more clear now. Imagine we upgrade from a server state machine:

  input -> state -> (output, state)

to a new version that has the following type:

  input' -> state' -> (output', state')

What would it take to still be able to serve old clients which make requests using the old input type? If we had a function from input -> input' we could upgrade the request, feed it to the new state machine and get an output' back, we then see that we’d also need a way to downgrade the output, i.e. a function output' -> output².

Forward compatibility, i.e. an upgraded client sends an input' to a server which haven’t been upgraded yet (i.e. expects input), is a bit more tricky, but again at least we can now start to be able to talk about these things in a more concrete way.

One last thing with regard to how to represent programs. Our state machines run entirely sequentially, which is a problem if we want to implement servers that can handle more than one client at the time. A simple way adding parallelism is make it possible to construct pipelines of state machines, where the state machines run in parallel. Picture the state machines as processing stages on a conveyor belt.

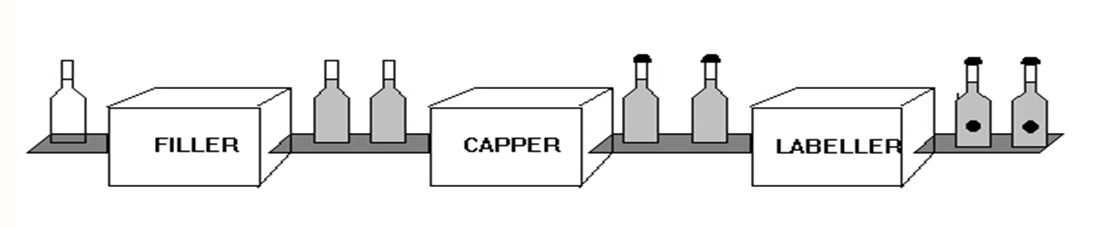
The conveyor belt in our case, i.e. our pipeline, will be queues which connect the state machines.

A typical TCP-based service can then be composed of a pipeline that:

1. Accepts new connections/sockets from a client;
2. Waits for some of the accepted sockets to be readable (this requires some select/poll/io_uring-like constructs);
3. recv the bytes of a request;
4. Deserialise the request bytes into an input;
5. Process the input using the a state machine to produce an output (potentially reading and writing to disk);
6. Serialise the output into a response in bytes;
7. Wait for the socket to be writable;
8. send the response bytes back to the client and close the socket.

Each of these stages could be a state machine which runs in parallel with all the other stages. Structuring services in this pipeline fashion was advocated by the late Jim Gray and more recently Martin Thompson et al have been giving talks using a similar approach. If a stage is slow, we can shard (or partition, using Jim’s terminology) it by dedicating another CPU/core to that stage and have even numbered requests to one CPU/core while odd numbered requests go to the other. That way we effectively double the throughput, without breaking determinism.

Let me just leave you with one final image. I like to think of state machines on top of pipelines as a limited form of actors or Erlang processes (gen_servers more precisely) that cannot send messages to which other process they like (graph-like structure), but rather only downstream (DAG-like structure)³.

Implementation

I hope that I’ve managed to convey what I’d like to do, why and where my inspiration is coming from.

Next I’d like to make things more concrete with some code. But first I’d like to apologies for my choice of using Haskell. I know it’s a language that not that many people are comfortable with, but its advanced type system (GADTs in particular) helps me express things more cleanly. If anything isn’t clear, feel free to ask, I’m happy to try to explain things in simpler terms. Also if anyone knows how to express this without GADTs, while retaining type safety, then please let me know. The code doesn’t add anything new to our previous discussion, merely validates that at least some of it can be implemented, so even if you can’t follow everything you won’t be missing out on anything important.

A few notes on the implementation:

• To keep things simple we’ll only implement linear pipelines. Each stage of the pipeline runs in parallel with all other stages, thus giving us pipelining parallelism à la assembly lines;
• The transformation at each stage is done via a state machine. The syntax of state machines needs to be easily serialisable, so that we can send upgrades over the wire;
• The remote end will need to deserialise and typecheck the receiving code in order to assure that it’s compatible with the already deployed code.

In the rest of this section we’ll try to fleshing out details of the above.

State machines

Typed state machines are represented using a datatype parametrised by the state, s, and indexed by its input type, a, and output type b⁴. For example the Identity state machine has the same input and output type, while if we want to Compose to state machines then output type of the first needs to be the same as the input type of the second, and so on.

data T s a b where
  -- Identity and composition.
  Id      :: T s a a
  Compose :: T s b c -> T s a b -> T s a c

  -- Introducing and incrementing integers.
  Int     :: Int -> T s () Int
  Incr    :: T s Int Int

  -- Mapping over sum types.
  Case    :: T s a c -> T s b d -> T s (Either a b) (Either c d)

  -- Read and update the state.
  Get     :: T s () s
  Put     :: T s s ()

  -- Converting values from and to strings.
  Read    :: Read a => T s String a
  Show    :: Show a => T s a String

-- Forward composition.
(>>>) :: T s a b -> T s b c -> T s a c
f >>> g = g `Compose` f

Example

To keep things concrete let’s reimplement the counter example from above.

type InputV1  = Either () ()
type OutputV1 = Either Int ()

pattern ReadCountV1 :: InputV1
pattern ReadCountV1 = Left ()

pattern IncrCountV1 :: InputV1
pattern IncrCountV1 = Right ()

counterV1 :: T Int String String
counterV1 = Read >>> counterV1' >>> Show
  where
    counterV1' :: T Int InputV1 OutputV1
    counterV1' = Get `Case` (Get >>> Incr >>> Put)

Notice how the two operations’ inputs and outputs are represented with an Either over which the Case operates.

Semantics

We can interpret our typed state machines in terms of the State monad as follows.

runT :: T s a b -> a -> s -> (b, s)
runT f x s = runState (eval f x) s

eval :: T s a b -> a -> State s b
eval Id            = return
eval (Compose g f) = eval g <=< eval f
eval (Int i)       = return . const i
eval Incr          = return . (+ 1)
eval (Case f g)    = either (fmap Left . eval f) (fmap Right . eval g)
eval Get           = const get
eval Put           = put
eval Read          = return . read
eval Show          = return . show

Using the above interpreter we can run our example from before.

> runT counterV1 (show ReadCountV1) 0
("Left 0",0)
> runT counterV1 (show IncrCountV1) 0
("Right ()",1)
> runT counterV1 (show ReadCountV1) 1
("Left 1",1)

These runs only step the counter by one input at the time, things get more interesting when state machines get streams of inputs via pipelines.

Pipelines

Pipelines are represented by a type similar to that for typed state machines, it’s also indexed by the input and output types.

We can picture a pipeline as a conveyor belt with state machines operating on the items passing through.

data P a b where
  IdP    :: P a a
  (:>>>) :: Typeable b => P a b -> P b c -> P a c
  SM     :: Typeable s => Name -> s -> T s a b -> P a b

type Name = String

Notice how the state type of the state machines is existentially quantified, meaning each state machine can have its own state.

Deployment

Pipelines can be deployed. Each state machine will be spawned on its own thread, meaning that all state machines run in parallel, and they will be connected via queues.

Given a pipeline P a b and an input Queue (Msg a) we get an output Queue (Msg b):

deploy :: forall a b. (Typeable a, Typeable b)
       => P a b -> Queue (Msg a) -> IO (Queue (Msg b))

where Msg is defined as follows.

data Msg a
  = Item (Maybe Socket) a
  | Upgrade (Maybe Socket) Name UpgradeData_
  ...

Think of Msg a as small wrapper around a which might contain a client socket (so that we know where to send the reply), or an upgrade. Upgrades are targeting a specific state machine in our pipeline, that’s what the Name parameter is for, and they also carry an untyped UpgradeData_ payload which will come back to shortly.

Given the above we can define deployment of pipelines as follows (I’ll explain each case below the code).

deploy IdP             q = return q
deploy (f :>>> g)      q = deploy g =<< deploy f q
deploy (SM name s0 f0) q = do
  q' <- newQueue
  let go :: Typeable s => s -> T s a b -> IO ()
      go s f = do
        m <- readQueue q
        case m of
          Item msock i -> do
            let (o, s') = runT f i s
            writeQueue q' (Item msock o)
            go s' f
          Upgrade msock name' ud
            | name /= name' -> do
                writeQueue q' (Upgrade msock name' ud)
                go s f
            | otherwise ->
                case typeCheckUpgrade f ud of
                  Just (UpgradeData (f' :: T t' a b) (g :: T () s t')) -> do
                    let (t', ()) = runT g s ()
                    case cast t' of
                      Just s' -> go s' f'
                      Nothing -> go s f
                  Nothing -> go s f
          ...
  _pid <- forkIO (go s0 f0)
  return q'

The identity pipeline simply returns the input queue. We deploy compositions of pipelines by deploying the components and connecting the queues. Deploying state machines is the interesting part.

When we deploy state machines, we first create a new queue which will hold the outputs, we then fork a new thread which reads from the input queue and writes to this new output queue, and finally we return the output queue. When reading from the input queue there’re two cases:

1. We can either get a regular Item in which case we step our state machine using the runT function to obtain an output and a new state, we write the output to the output queue and continue processing with the new state;
2. Or, if the Msg is an Upgrade we first check if the upgrade is targeting this state machine by checking if the names match, if not we simply pass it further downstream. If the names to match then we try to typecheck the untyped UpgradeData_. If the typechecking succeeds, we’ll get a new state machine and a state migration function, which allows us to migrate the current state and continue processing with the new state machine.

Next let’s have a look at how upgrades are represented and typechecked.

Upgrades

Upgrades are sent over the wire in a serialised format and deserialised at the other end, so they need to be plain first-order data.

This means we can’t merely send over our typed state machine type t :: T s a b, or rather the receiver will have to reconstruct the type information. If this sounds strange, the perhaps easiest way to convince yourself is to imagine you receive show t and now you want to reconstruct t. When you call read (show t) you need to annotate it with what type to read into, and that’s the problem: at this point you don’t have the type annotation T s a b.

So the plan around this is to introduce a plain first-order datatype for upgrades, which can easily be serialised and deserialised, and then use typechecking to reconstruct the type information.

data UpgradeData_ = UpgradeData_
  { oldState        :: Ty_
  , newState        :: Ty_
  , newInput        :: Ty_
  , newOutput       :: Ty_
  , newStateMachine :: U
  , stateMigration  :: U
  }
  deriving (Show, Read)

We can to typecheck the above untyped upgrade into the following typed version.

data UpgradeData s a b = forall s'. Typeable s' =>
  UpgradeData (T s' a b) (T () s s')

The way typechecking for upgrades work is basically the user needs to provide the untyped types of the state, input and output types of the new state machine as well as the state migration function, from the untyped types we can infer the typed types which we then typecheck the new state machine and migration function against.

typeCheckUpgrade :: forall s a b. (Typeable s, Typeable a, Typeable b)
                 => T s a b -> UpgradeData_ -> Maybe (UpgradeData s a b)
typeCheckUpgrade _f (UpgradeData_ t_ t'_ a'_ b'_ f_ g_) =
  case (inferTy t_, inferTy t'_, inferTy a'_, inferTy b'_) of
    (ETy (t :: Ty t), ETy (t' :: Ty t'), ETy (a' :: Ty a'), ETy (b' :: Ty b')) -> do
      Refl <- decT @a @a'
      Refl <- decT @b @b'
      Refl <- decT @s @t
      f <- typeCheck f_ t' a' b'
      g <- typeCheck g_ TUnit t t'
      return (UpgradeData f g)

Where untyped types are defined as follows:

data Ty_
  = UTUnit
  | UTInt
  | UTBool
  | UTString
  | UTPair Ty_ Ty_
  | UTEither Ty_ Ty_

and typed types as follows:

data Ty a where
  TUnit   :: Ty ()
  TInt    :: Ty Int
  TBool   :: Ty Bool
  TString :: Ty String
  TPair   :: Ty a -> Ty b -> Ty (a, b)
  TEither :: Ty a -> Ty b -> Ty (Either a b)
  ...

and the way we infer typed types from the untyped ones is done as follows:

data ETy where
  ETy :: Typeable a => Ty a -> ETy

inferTy :: Ty_ -> ETy
inferTy UTUnit = ETy TUnit
inferTy UTInt  = ETy TInt
inferTy UTBool = ETy TBool
inferTy UTString = ETy TString
inferTy (UTPair ua ub) = case (inferTy ua, inferTy ub) of
  (ETy a, ETy b) -> ETy (TPair a b)
inferTy (UTEither ua ub) = case (inferTy ua, inferTy ub) of
  (ETy a, ETy b) -> ETy (TEither a b)

Now the only piece missing is untyped state machines and how to typecheck those into typed ones.

typeCheck :: U -> Ty s -> Ty a -> Ty b -> Maybe (T s a b)

data U
  = IdU
  | ComposeU U U
  | IntU Int
  | CaseU U U
  | IncrU
  | GetU
  | PutU
  | ReadU Ty_
  | ShowU Ty_

I’ll spare you from the details, but the main ingredient is to use the Data.Typeable instances to check if the types match up, similarly to how it was done above in typeCheckUpgrade.

Sources and sinks

Almost there. When we deploy a pipeline P a b we need to provide a Queue (Msg a) and get a Queue (Msg b), what are we supposed to do with those queues? We could manually feed them with items, but for convenience it’s nice to have some basic reusable adapters that we can connect these “garden hoses” to.

We call something that provides an input queue a Source and something that consumes an output queue a Sink. Useful sources and sinks include stdin/stdout, files, and TCP streams.

We can then implement a run function with the following type:

run :: (Typeable a, Typeable b)
    => Source a -> Codec (Msg a) (Msg b) -> P a b -> Sink b r -> IO r

Where Codec a b contains a deserialiser from ByteString to Maybe a and a serialiser from b to ByteString. We need this because our sources and sinks produce and consume ByteStrings.

Remote upgrades

Putting it all together we can now create a TCP server for our counter:

run (FromTCP "127.0.0.1" 3000) readShowCodec (SM "counter" 0 counterV1) ToTCP

If we run the above in a REPL, then from another terminal we can interact with the server as follows.

# Get the current state of the counter.
$ echo 'Item "Left ()"' | nc 127.0.0.1 3000
Item "Left 0"

# Increment the counter.
$ echo 'Item "Right ()"' | nc 127.0.0.1 3000
Item "Right ()"

# Read the counter again.
$ echo 'Item "Left ()"' | nc 127.0.0.1 3000
Item "Left 1"

In order to make life a bit easier for ourselves, we can implement a simple TCP client in Haskell and use from another REPL to achieve the same result.

nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV1))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV1))
nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV1))
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV1))

Item "Left 0"               -- The initial value of the counter is 0.
Item "Right ()"             -- Two increments.
Item "Right ()"
Item "Left 2"               -- The value is now 2

At this point, let’s imagine we want to add a reset feature to our counter. Reset takes no argument and returns nothing, so we use the unit type in both the input and output types.

type InputV2  = Either () InputV1
type OutputV2 = Either () OutputV1

pattern ResetCountV2 :: InputV2
pattern ResetCountV2 = Left ()

pattern ReadCountV2 :: InputV2
pattern ReadCountV2  = Right ReadCountV1

pattern IncrCountV2 :: InputV2
pattern IncrCountV2  = Right IncrCountV1

The state machine looks the same, except for the first Case where we update the state to be 0, thus resetting the counter.

counterV2 :: T Int String String
counterV2 = Read >>> counterV2' >>> Show
  where
    counterV2' :: T Int InputV2 OutputV2
    counterV2' =
      (Int 0 >>> Put) `Case`
      Get `Case`
      (Get >>> Incr >>> Put)

Back in our REPL we can now do the upgrade, by sending over a type erased version of counterV2.

let msg :: Msg ()
    msg = Upgrade Nothing "counter"
            (UpgradeData_ UTInt UTInt UTString UTString (erase counterV2) (erase Id))
nc "127.0.0.1" 3000 msg

nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV2))
nc "127.0.0.1" 3000 (Item Nothing (show ResetCountV2))
nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV2))

Which yields the following annotated output.

UpgradeSucceeded "counter"
Item "Right (Left 2)"   -- The counter's state is preserved by the upgrade.
Item "Left ()"          -- Reset the counter.
Item "Right (Left 0)"   -- The value is back to 0.

As a final example of an upgrade, let’s do a more interesting state migration. Let’s say we want to add a boolean to the state which determines if IncrCount should add by 1 or -1 (i.e. decrement). This boolean can be toggled by the user using a new operation, while the signatures of the other operations stay the same as before.

type InputV3  = Either () InputV2
type OutputV3 = Either () OutputV2

pattern ToggleCountV3 :: InputV3
pattern ToggleCountV3 = Left ()

pattern ReadCountV3, IncrCountV3, ToggleCountV3 :: InputV3

In order to implement the toggle operation we need to extend the syntax of our state machines to be able to deal with booleans and products (the details can be found here).

counterV3 :: T (Int, Bool) String String
counterV3 = Read >>> counterV3' >>> Show
  where
    counterV3' :: T (Int, Bool) InputV3 OutputV3
    counterV3' =
      -- Toggle negates the boolean in the state (the second component).
      (Get >>> Second Not >>> Put) `Case`
      -- Reset resets the counter and the boolean back to false (i.e. incrementing).
      (Int 0 :&&& Bool False >>> Put) `Case`
      -- Reading the counter picks out the first component from the state.
      (Get >>> Fst) `Case`
      -- Incrementing or decrementing, depending on the boolean in the state.
      (Get >>> If Decr Incr >>> (Id :&&& (Consume >>> Get >>> Snd)) >>> Put)

We can then upgrade to our new version of the counter as follows.

  let msg2 :: Msg ()
      msg2 = Upgrade Nothing "counter"
               (UpgradeData_ UTInt (UTPair UTInt UTBool) UTString UTString
                 (erase counterV3) (erase (Id :&&& Bool False)))
  nc "127.0.0.1" 3000 msg2

Notice how the state is migrated using Id :&&& Bool False, i.e. create a pair where the first component is the old value of the state (this is the current count) and the second component is False (this is whether we are decrementing).

Here’s a final example of how we can use the new counter.

  nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV3))
  nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV3))
  nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV3))
  nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV3))
  nc "127.0.0.1" 3000 (Item Nothing (show ToggleCountV3))
  nc "127.0.0.1" 3000 (Item Nothing (show IncrCountV3))
  nc "127.0.0.1" 3000 (Item Nothing (show ReadCountV3))

The above yields the following output.

UpgradeSucceeded "counter"
Item "Right (Right (Left 0))"   -- The counter is 0.
Item "Right (Right (Right ()))" -- Two increments.
Item "Right (Right (Right ()))"
Item "Right (Right (Left 2))"   -- The counter is 2.
Item "Left ()"                  -- Toggle to decrementing.
Item "Right (Right (Right ()))" -- Decrement.
Item "Right (Right (Left 1))"   -- The value is 1.

Discussion and future work

If we look back at the list, from the introduction, of properties that we wanted from our upgrades, then I hope that I’ve managed to provide a glimpse of a possible way of achieving zero-downtime upgrades with type-safe state migrations that are atomic.

Downgrades can be thought of as an upgrade to an earlier version, although it could be interesting to experiment with requiring an inverse function to the state migration as part of an upgrade. That way the system itself could downgrade in case there’s more than N errors within some time period, or something like that.

I didn’t talk about backwards and forwards compatibility. We could probably use an interface description language, such as Avro or Protobuf, but it could also be interesting see if we could add input and output migrations as part of upgrades (in addition to state migrations). Especially in conjunction with being able to derive them generically and automatically from the schema change.

There’s also a bunch of other things that I thought of while working on this, which I don’t have any good answers for yet. If you feel that I’m missing something, or if you know some answers or if any of these problems sound interesting to work on, please do feel free to get in touch!

Let me close by trying to tie it back to Barbara Liskov’s remark about the need for more complete programming languages. In a world where software systems are expected to evolve over time, wouldn’t it be neat if programming languages provided some notion of upgrade and could typecheck our code across versions, as opposed to merely typechecking a version of the code in isolation from the next?