Scheduling threads like Thomas Jefferson

Background and motivation

You know how assembly lines in manufacturing and instruction pipelines in CPUs give a form of parallelism, without breaking determinism (the order of inputs to the pipeline is preserved in the outputs)?

We’ll call this implicit parallelism via pipelining. Implicit, because by merely splitting the task at hand up in stages, we get parallelism for free. When this technique is applied to software, it allows us to write purely sequential programs (for each stage), while still utilising our parallel hardware.

The way it works is that each stage runs independently (one CPU/core) and the stages are connected via queues, so when the first CPU/core is done with the first stage of the first item, it passes it on to the second stage while continuing to work at the first stage of the second item. As the queues between the stages saturate we get parallelism while retaining determinism (the outputs arrive in the same order as the inputs).

Here’s a picture of a bottle factory manufacturing pipeline:

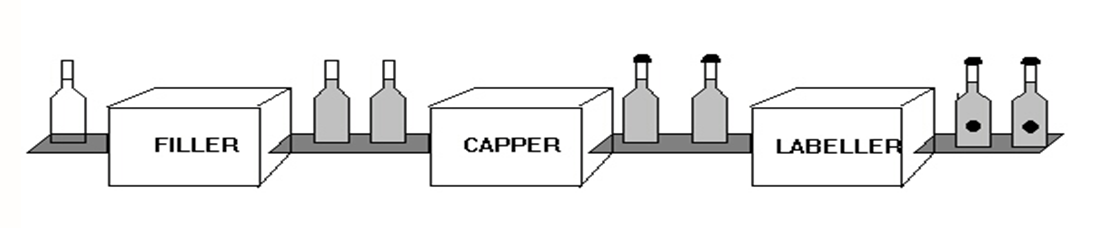
Each stage is connected by conveyor belts (queues) and runs in parallel with the other, e.g. after as the first bottle has been filled, the second can be filled while at the same time the first bottle is being capped, etc.

If a stage is slow, then an input queue to the stage can be partitioned or sharded by adding another worker to that stage sending every other input to the newly added worker, thereby effectively nearly doubling the throughput.

In this post I’d like to discuss the following question: what’s the best way to allocate CPUs/cores among the stages? For example, if we only have two CPUs/cores, but three stages, then it doesn’t make any sense to allocate one of them to the last stage until at least some items has been processed at the second stage.

First I’d like to develop a library to test out these concepts, but longer term I’d like to make a programming language which uses these concepts to try see if we can make something that scales well as more CPUs/cores are available.

Inspiration and prior work

While there are examples of pipelining in manufacturing that pre-date Henry Ford, it seems that’s when it took off and became commonplace. Wikipedia says:

“The assembly line, driven by conveyor belts, reduced production time for a Model T to just 93 minutes by dividing the process into 45 steps. Producing cars quicker than paint of the day could dry, it had an immense influence on the world.”

For comparison, it apparently took 12.5h before the assembly line.

CPUs are another example where pipelining is used, with the intent of speeding up the processing of instructions. A pipeline might look like: fetch the instruction, fetch the operands, do the instruction, and finally write the results.

Given this tremendous success in both manufacturing and hardware one could expect that perhaps it’s worth doing in software as well? For reasons not entirely clear to me, it doesn’t seem to have taken off yet, but there are proponents of this idea.

Jim Gray talked about software pipeline parallelism and partitioning in his Turing award interview. Dataflow languages in general and Paul Morrison’s flow-based programming in particular exploit this idea. The LMAX Disruptor pattern is also based on pipelining parallelism and supports, what Jim calls, partition parallelism. One of the sources that the Disruptor paper mentions is SEDA: An Architecture for Well-Conditioned, Scalable Internet Services (2001), which also talks about pipelines and dynamically allocating threads to the stages. More recently, as I was digging into more of Jim’s work, I discovered that database engines also implement something akin to pipeline parallelism. For a more recent example of database engines that use this technique, see the paper on Umbra’s morsel-driven parallelism (2014).

These are the examples of software pipeline parallelism that inspired me to start thinking about it. However it wasn’t until I read Martin Thompson, one of the people behind the LMAX Disruptor, say the following:

“If there’s one thing I’d say to the Erlang folks, it’s you got the stuff right from a high-level, but you need to invest in your messaging infrastructure so it’s super fast, super efficient and obeys all the right properties to let this stuff work really well.”

Together with hearing Joe Armstrong’s anecdote of an unmodified Erlang program only running 33 times faster on a 64 core machine, rather than 64 times faster as per the Ericsson higher-up’s expectations, that I started thinking about how a programming language can be designed to make it easier to do pipelining in software.

I started exploring this topic in two of my previous posts, and I’ve also written about elastically scaling a single stage up and down before, but here we’ll take a more global approach.

Big picture

The system consists of three parts: the pipeline, the workers and the scheduler:

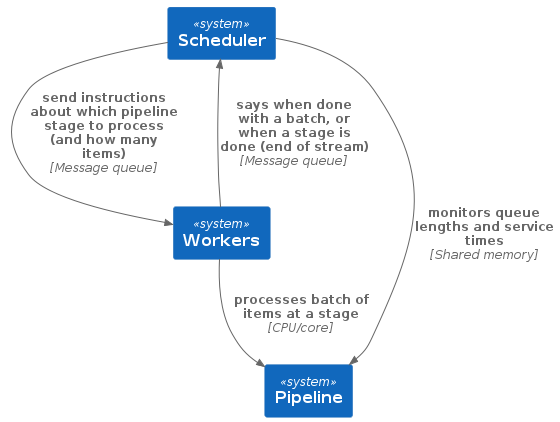
The scheduler monitors the pipeline, looking at how long the input queue for each stage is and what the average service time per input of that stage is. By doing so it calculates where to schedule the available workers.

The algorithm to allocate the available workers works as follows:

1. Generate all possible configurations of allocating workers across the stages;
2. Score each configuration using the formula: \(\sum_{s}\frac{l_{s} \cdot t_{s}}{w_{s} + 1}\), where \(s\) is a stage, \(l_{s}\) is the input queue length of the stage \(s\), \(t_{s}\) is the average service time of the stage \(s\) and \(w_{s}\) is the amount of workers allocated to the stage \(s\);
3. Pick the configuration with the lowest score, i.e. the one where the total processing time is the lowest.

The workers, typically one per available CPU/core, process a batch of inputs at the stage the scheduler instructs them to and then report back to the scheduler, and so the process repeats until the end of the stream of inputs.

If we zoom in on the pipeline, we see that it consists of a source, N stages and a sink:

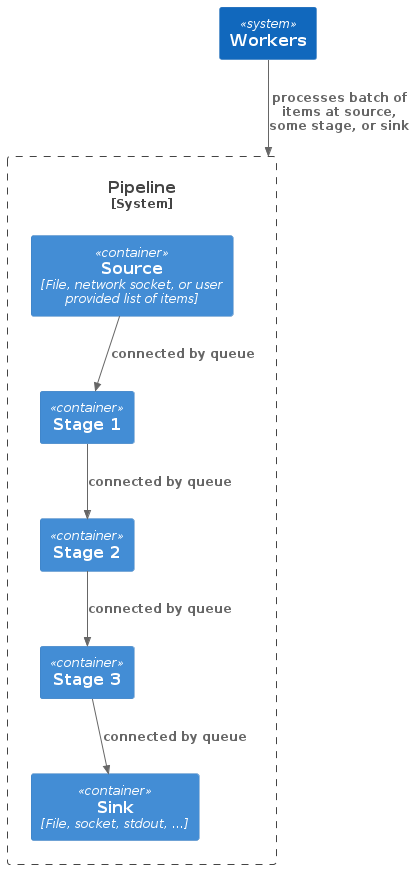
The source can be a file, network socket, a user provided list of items, etc, from which the inputs to the queue of the first stage are created. The inputs can be length-prefixed raw bytes, or newline-separated bytes, etc. Similarly the sink can also be a file, or standard out, or a socket. While in between the source and the sink is where the interesting processing happens in stages.

Prototype implementation

From the above picture, I hope that it’s clear that most of the code is plumbing (connecting the components with queues). The most interesting aspect of the code is: when a worker is done, how does the scheduler figure out what it shall tell it to do next? So let’s focus on that.

We start off by representing what a configuration of workers across a pipeline looks like. Each stage has a name, or identifier, and so a configuration can be represented as a map from the stage identifier to the number of workers assigned to that stage:

newtype Config = Config (Map StageId NumOfWorkers)
  deriving Show

type NumOfWorkers = Int

The initial configuration is that all stages have zero workers assigned to it:

initConfig :: [StageId] -> Config
initConfig stageIds =
  Config (Map.fromList (zip stageIds (replicate (length stageIds) 0)))

The implementation for allocating workers starts by generating all possible configurations, filters away configurations which allocate workers to stages that are done (where done means that no further inputs will arrive to that stage), scores all the configurations and picks the one with the lowest score:

allocateWorkers :: Int -> Map StageId QueueStats -> Set StageId -> Maybe Config
allocateWorkers cpus qstats done = case result of
  []                -> Nothing
  (cfg, _score) : _ -> Just cfg
  where
    result = sortBy (comparing snd)
               [ (cfg, sum (Map.elems (scores qstats cfg)))
               | cfg <- possibleConfigs cpus (Map.keys qstats)
               , not (allocatesDoneStages cfg done)
               ]

All possible configurations are generated as follows:

possibleConfigs :: Int -> [StageId] -> [Config]
possibleConfigs cpus stages = map (Config . Map.fromList . zip stages) $ filter ((== cpus) . sum)
  [ foldl' (\ih i -> update i succ ih) (replicate (length stages) 0) slot
  | choice <- combinations [0.. (cpus + length stages - 1)] cpus
  , let slot = [ c - i | (i, c) <- zip [0.. ] choice ]
  ]
  where
    combinations :: [a] -> Int -> [[a]]
    combinations xs n = filter ((== n) . length) (subsequences xs)

    -- update i f xs = xs[i] := f (xs[i])
    update :: Int -> (a -> a) -> [a] -> [a]
    update i f = go [] i
      where
        go acc _ []       = reverse acc
        go acc 0 (x : xs) = reverse acc ++ f x : xs
        go acc n (x : xs) = go (x : acc) (n - 1) xs

While scoring is implemented as following:

scores :: Map StageId QueueStats -> Config -> Map StageId Double
scores qss (Config cfg) = joinMapsWith score qss cfg
  where
    score :: QueueStats -> Int -> Double
    score qs workers =
      (fromIntegral (queueLength qs) * fromIntegral avgServiceTimePicos)
      /
      (fromIntegral workers + 1)
      where
        avgServiceTimePicos :: Word64
        avgServiceTimePicos
          | len == 0  = 1 -- XXX: What's the right value here?
          | otherwise = sum (serviceTimesPicos qs) `div` len
          where
            len :: Word64
            len = genericLength (serviceTimesPicos qs)

Where a small helper function is used to join maps:

joinMapsWith :: Ord k => (a -> b -> c) -> Map k a -> Map k b -> Map k c
joinMapsWith f m1 m2 = assert (Map.keys m1 == Map.keys m2) $
  Map.fromList
    [ (k, f x (m2 Map.! k))
    | (k, x) <- Map.toList m1
    ]

The last piece we need is to be able to tell when a configuration allocates workers to a stage that’s done:

allocatesDoneStages :: Config -> Set StageId -> Bool
allocatesDoneStages (Config cfg) done =
  any (\(stageId, numWorkers) -> stageId `Set.member` done && numWorkers > 0)
      (Map.toList cfg)

Running the prototype

Let’s finish off with a couple of examples in the REPL. Let’s say we have two workers, and two stages (\(A\) and \(B\)), the \(A\) stage has three items on its input queue (and this will be all the inputs it will receive), and no stage is done yet (that’s the last S.empty argument):

>>> allocateWorkers 2 
                    (M.fromList [ ("A", QueueStats 3 [])
                                , ("B", QueueStats 0 [])]) 
                    S.empty

(The QueueStats constructor takes the input queue length as first argument and a list of service times as second argument.)

If we run the above, we get:

Just (Config (fromList [("A",2),("B",0)]))

Which means both workers should be allocated to the \(A\) stage. Let’s say that we do that allocation and after 1 time unit passes both workers finish, that means that the \(A\) input queue now has one item left on it, while the second stage (\(B\)) now has two items on its input queue. Since both workers are done, we rerun the allocation function:

>>> allocateWorkers 2 
                    (M.fromList [ ("A", QueueStats 1 [1,1])
                                , ("B", QueueStats 2 [])]) 
                    S.empty
Just (Config (fromList [("A",1),("B",1)]))

The result now is that we should allocate one worker to each stage. If we again imagine that we do so and they both finish after one time unit, we end up in a situation where all three items have been processed from the first stage (\(A\)), so we can mark \(A\) as done, while the second stage will have two items on its input queue:

>>> allocateWorkers 2 
                    (M.fromList [ ("A", QueueStats 0 [1,1,1])
                                , ("B", QueueStats 2 [1])]) 
                    (S.fromList ["A"])
Just (Config (fromList [("A",0),("B",2)]))

Allocating workers at this point will allocate both to the second stage. After the workers finished working on those items the second stage will have processed all items as well and we are done:

>>> allocateWorkers 2 
                    (M.fromList [ ("A", QueueStats 0 [1,1,1])
                                , ("B", QueueStats 0 [1,1,1])]) 
                    (S.fromList ["A", "B"])
Nothing

Unexpected connection to Thomas Jefferson

As I came up with this idea of scheduling described above, I bounced it off my friend Daniel Gustafsson who immediately replied “this reminds me a bit of Jefferson’s method” (of allocating seats in parliaments).

Here’s how the process works:

“After all the votes have been tallied, successive quotients are calculated for each party. The party with the largest quotient wins one seat, and its quotient is recalculated. This is repeated until the required number of seats is filled. The formula for the quotient is:

\(quot = \frac{V}{s + 1}\)

where:

• V is the total number of votes that party received, and
• s is the number of seats that party has been allocated so far, initially 0 for all parties.”

The analogy being:

parties         : stages in the pipeline
seats per party : workers allocated to a stage
votes           : "score" (= length of input queue times average service time)
rounds          : total number of workers

Let’s try to redo the example from above, where the stage \(A\) and \(B\) had queue length of \(1\) and \(2\) respectively, but using the Jefferson method:

1. In the first round, party/stage \(A\) gets \(1\) vote, while party \(B\) gets \(2\) votes, so the quotient is \(\frac{1}{0 + 1}\) and \(\frac{2}{0 + 1}\) respectively, which means that stage \(B\) wins the round and gets allocated a seat;

2. In the second round we get the quotients: \(\frac{1}{0 + 1} = 1\) and \(\frac{2}{1 + 1} = 1\) (note that \(s = 1\) here, because stage/party \(B\) already won a seat in the previous round). Which means we get a tie, in this case I guess we could arbitrarily pick the first party, just so that our example works out the same as in the implementation¹.

Daniel also explained that while Jefferson came up with this method, it’s not actually used in the USA, but in most of Europe including the EU parliament use the method.

Conclusion and future work

We’ve seen a strategy of how one can elastically scale the amount of CPUs/cores dedicated to one stage in a pipeline. Being able to do so should come handy if:

1. The load on the system changes and suddenly one stage becomes slower than another, by being elastic we can rebalance the cores and maintain throughput;
2. The load decreases, we can scale down and use the cores elsewhere in the system.

We also saw how Thomas Jefferson’s method of allocating seats in a parliament can be used to solve the same problem. This unexpected connection makes me wonder where else this algorithm pops up?

We are still far from being able to implement a parallel programming language runtime using these ideas. In particular the current implementation uses simple concurrent queues to connect the stages, meaning that scaling up a stage doesn’t preserve determinism of the output. This can be solved using Disruptors instead, as in my older post. I’ve collected a bunch of other things left to do in a separate file. If any of this interests you, feel free to get in touch.